Latest

6/recent/ticker-posts

CHAPTER 3: MAP METHOD- MORRIS MANO-2ND EDITION SOLUTION

Xobdo_Sum October 03, 2020

NOTE: If you have any queries regarding the solutions, feel free to comment down. 

1.       3.1: Simplify the following boolean functions using three-variable maps:

a)      a. F(x,y,z)=∑(0,1,5,7)

 

   Solution:-


    Therefore, F=xz+x’y’

b) F(x,y,z)=∑(1,2,3,6,7)

Solution:-

         Therefore, F=x’z+y

c)   F(x,y,z)=∑(3,5,6,7)

           Therefore, F=xy+yz+xz.

d)  F(A,B,C) =∑(0,2,3,4,6)

              



     F=C’+A’B

3. 2. Simplify the following Boolean expressions using three-variable maps:

 a.                xy+x’y’z’+x’yz’

Solution:-


            F=x’z’+xy

b.      x’y’+yz+ x’yz’

        Therefore, F= x’+yz

c.      A’B+BC’+B’C’

          F=C’+A’B

 3.3.      Simplify the following Boolean functions using four-variable maps:

a.      F(A,B,C,D)=∑(4,6,7,15)

        Therefore, F=A’BD’+BCD

 

b. F(w,x,y,z)=∑(2,3,12,13,14,15)


        F= wx+w’x’y


c. F(A,B,C,D)=∑(3,7,11,13,14,15)

        F=CD+ABD+ABC

3.4. Simplify the following Boolean functions using four variable maps:


a.                F(w,x,y,z)=∑(1,4,5,6,12,14,15)



        F=xz’+w’y’z+wxy

 b. F(A,B,C,D)=∑(0,1,2,4,5,7,11,15)

        F=A’B’D’+A’C’+BCD+ACD


c. F(w,x,y,z)=∑(2,3,10,11,12,13,14,15)   


         F=wx+x’y

 

d. F(A,B,C,D)=∑(0,2,4,5,6,7,8,10,13,15)




        F=BD+B’D’+A’D’

3.5. Simplify the following Boolean expressions using four-variable maps:


a.                w’z+xz+x’y+wx’z



            F=z+x’y


b. B’D+A’BC’+AB’C+ABC’




        F=BC’+B’D+AB’C


c. AB’C+B’C’D’+BCD+ACD’+A’B’C+A’BC’D




        F=B’D’+CD+AC+A’BD

 

 d. wxy+yz+xy’z+x’y


    F=x’y+wy+xz

 

3.6. Find the minterms of following Boolean expressions by first plotting each function in a map:

 

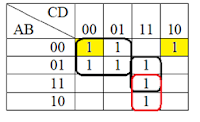
a)      xy+yz+xy’z



 

yz

 

 

 

 

x

 

00

01

11

10

 

0

 

 

1

 

 

1

 

1

1

1

                                     F=∑(3,5,6,7)

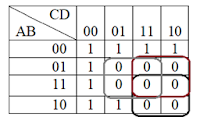
b. CD’+ABC’+ABD’+A’B’D

 

 

CD

 

 

 

 

AB

 

00

01

11

10

 

00

 

1

1

1

 

01

 

 

 

1

 

11

1

1

 

1

 

10

 

 

 

1

                                     F=∑(1,2,3,6,10,12,13,14)

 

c. wxy+x’z’+w’xz

 

 

yz

 

 

 

 

wx

 

00

01

11

10

 

00

1

 

 

1

 

01

 

1

1

 

 

11

 

 

1

1

 

10

1

 

 

1

 

                                 F=∑(0,2,5,7,8,10,14,15)


3.7. Simplify the following Boolean expressions by first finding the essential prime implicants.

 

a.                F(w,x,y,z)=∑(0,2,4,5,6,7,8,10,13,15)



The essential prime implicants are xz and x’z’

        F=xz+x’z’+w’x

b. F(A,B,C,D)=∑(0,2,3,5,7,8,10,11,14,15)



The essential prime implicants are AC, B’D’,A’BD

F=AC+B’D’+A’BD+CD

 

c. F(A,B,C,D)=∑(1,3,4,5,10,11,12,13,14,15)



The essential prime implicants are BC’ and AC

F=BC’+AC+A’B’D


3.8. Simplify the following Boolean functions using five-variable maps:

 

a.                F(A,B,C,D,E)=∑(0,1,4,5,16,17,21,25,29)



        F=A’B’D’+AD’E+B’C’D’

 b. F(A,B,C,D,E)=∑(0,2,3,4,5,6,7,11,15,16,18,19,23,27,31)


        F=A’B’C+DE+B’C’E’

 

 c. F=A’B’CE’+A’B’C’D’+B’D’E’+B’CD’+CDE’+BDE’


        F=D’E’+B’D’

3.9. Simplify the following Boolean functions in product of sum:

 

a.                F(w,x,y,z)=∑(0,2,5,6,7,8,10)





    F’=x’z+wx+xy’z’

    F=(x+z’)(w’+x’)(x’+y+z)

b. F(A,B,C,D)=∏(1,3,5,7,13,15)


        F’=A’D+BD

        F=(A+D’)(B’+D’)

c. F(x,y,z)=∑(2,3,6,7)


        F’=y’

        F=y

d. F(A,B,C,D)=∏(0,1,2,3,4,10,11)

         F’=B’C+A’B’+A’C’D’

             F=(B+C’)(A+B)(A+C+D)

3.10. Simplify the following expressions in (i)sum of products (ii)products of products:


a.                x’z’+y’z’+yz’+xy


        F=xy+z’

        F’=y’z+x’z

        F=(y+z’)(x+z’)

 

 b. AC’+B’D+A’CD+ABCD


        F=AC’+CD+A’D

        F’=CD’+A’D’+A’BC’

        F=(C’+D)(A+D)(A+B’+C)

c. (A’+B’+D’)(A+B’+C’)(A’+B+D’)(B+C’+D’)



        F=AD’+A’C’

        F’=AD+C’D’+A’BC

        F=(A’+D’)(C+D)(A+B’+C’)


3.11. Draw the AND-OR gate implementation of the following function after simplifying it in (a)sum of products and (b) product of sums:

F(A,B,C,D)=∑(0,2,5,6,7,8,10)



        F=B’D’+A’BD+A’BC

        F’=B’D+AB+BC’D’

        F=(B+D’)(A’+B’)(B’+C+D)

 

3.12. Simplify the following expressions and implement them with two-level NAND gate circuits:


a.                AB’+ABD+ABD’+A’C’D’+A’BC’



        F=A+BC’+C’D’





b. BD+BCD’+AB’C’D’




        BD+BC+AB’C’D’ 



3.13. Draw a NAND logic diagram that implements the complements of the following function:

F(A,B,C,D)=∑(0,1,2,3,4,8,9,12)


        F’=BD+BC+AC

 

3.14. Draw a logic diagram using only two-input NAND gates to implement the following  

      expression:

    (AB+A’B’)(CD’+C’D)


3.15. Simplify the following functions and implement them with two-level NOR gate circuits:


a.     F=wx’+y’z’+w’yz’


        F’=w’z+xz+wxy

        F=(w+z’)(x’+z’)(w’+x’+y’)





b. F=(w,x,y,z)=∑(5,6,9,10)



        F’=w’x’+wx+y’z’+yz

        F=(w+x)(w’+x’)(y+z)(y’+z’)




3.16. Implement the functions of problem 15 with three level NOR gate circuits

 

a.    F=wx’+y’z’+w’yz’


    F’=(w’+x)(y+z)(w+y’+z)


    And F=(F’)’




b. F=(w,x,y,z)=∑(5,6,9,10)


 

 

 

yz

 

 

 

 

wx

 

00

01

11

10

 

00

 

 

 

 

 

01

 

1

 

1

 

11

 

 

 

 

 

10

 

1

 

1

 

F=w’xy’z+w’xyz’+wx’y’z+wx’yz’

F’=(w+x’+y+z’)(w+x’+y’+z)(w’+x+y+z’)(w’+x+y’+z)






 

3. 17. Implement the expressions of problem 12 with three-level NAND circuits:

a.      F=AB’+ABD+ABD’+A’C’D’+A’BC’


         F’=A’C+A’B’D

         F=(F’)’




b. F=BD+BCD’+AB’C’D’



        F’=B’C+B’D+A’C’D’+BC’D’




3.18. Give three possible ways to express the function F with eight or fewer literals

F(A,B,C,D)=∑(0,2,5,7,10,13)


    

    F=A’B’D’+B’CD’+A’BD+BC’D

    F=B’D’(A+C)+BD(A’+C’)                                  (1ST WAY)

    F’=BD’+B’D+ABC+AB’C’

        =B(D’+AC)+B’(D+AC’)

     F=(B’+D(A’+C’))+(B+D’(A’+C))                      (2ND WAY)

 


       

        F’=BD’+B’D+AC’D’+ACD

            =D’(B+AC’)+D(B’+AC)

        F=(D+B’(A’+C))(D’+B(A’+C’))                                        (3RD WAY)


 

3.19. Find eight different two level gates circuits to implement F=xy’z+x’yz+w


F=w+x’yz+xy’z


        AND-OR implementation

        NAND –NAND implementation

 

F’=w’z’+w’x’y’+w’xy

F=(w+z)(w+x+y)(w+x’+y’)

        OR-AND implementation

          NOR-NOR implementation

F=xy’z+x’yz+w

F=((x’+y+z’)(x+y’+z’)(w’))’


        NOR-OR implementation

        OR-NAND

F’=w’z’+w’x’y’+w’xy

F=(w’z’+w’x’y’+w’xy)’

        NAND-AND implementation

        AND-NOR implementation

3.20: implement the function F with the following two level forms- NAND-AND, AND-NOR, OR-NAND, NOR-OR.

F(A,B,C,D)=m0+m1+m2+m3+m4+m8+m9+m12



F=C’D’+A’B’+B’C’

F=((C+D)(A+B)(B+C))’

F’=AC+BC+BD

F=(A’+C’)(B’+C’)(B’+D’)

F=(AC+BC+BD)’

            NAND-AND 

            AND-NOR

            OR-NAND

            NOR-OR





3.21: List the eight degenerate two level forms and show that they reduce to a single operation. Explain how the degenerate two level forms can be used to extend the number of inputs to a gate.

AND-OR

OR-AND

NAND-NAND

NOR-NOR

NOR-OR

NAND-AND

OR-NAND

AND-NOR

The degenerate two level forms can be used to extend the number of inputs to a gate as using these forms we can get a single operation effectively.



3.22: Simplify the Boolean function F together with the don’t care conditions d, then express the simplified function in sum of minterms.

a) F(x,y,z)=m0+m1+m2+m4+m5

    d(x,y,z)=d3+d6+d7

 



F=1

F=m0+m1+m2+m3+m4+m5+m6+m7

b)F(A,B,C,D)=m0+m6+m8+m13+m14

   d(A,B,C,D)=d2+d4+d10



F=B’D’+CD’+ABC’D

F=m0+m2+m6+m8+m13+m14

 

c) F(A,B,C,D)=m1+m3+m5+m7+m9+m15

    d(A,B,C,D)=d4+d6+d12+d13

    

               F=C’D+BD+A’D

               F=m1+m3+m5+m7+m9+m13+m14

 3.23: Simplify the Boolean function F together with the don’t care conditions d (i) sum of products

(ii) product of sum

a)      F(w,x,y,z)=  m0+m1+m2+m3+m7+m8+m10    

      d(w,x,y,z)=d5+d6+d11+d15

 

      F=x’z’+w’z

F’=xz’+wz

F=(x’+z)(w’+z’)

 

 

b)    b)   F(A,B,C,D)=m3+m4+m13+m15

d(A,B,C,D)= d1+d2+d5+d6+d8+d10+d12+d14



F=BD’+AB+A’B’D

F’=B’D’+AB’+A’BD

F=(B+D)(A’+B)(A+B’+D’)

3.24: A logic circuit implement the following Boolean function F=A’C+AC’D’

It is found that the circuit input combination A=C=1 can never occur. Find a simpler expression for F using the proper don’t care conditions.

Solution: 

The don’t care terms will be  d=AC


 


F=C+AD’

3.25: Implement the following Boolean function F together with the  don’t care conditions d using no more than two NOR gates. Assume that both the normal and complement inputs are available.

F(A,B,C,D)=(m0+m1+m2+m9+m11)

d(A,B,C,D)=(d8+d10+d14+d15)


F’=B+A’CD

F=B’(A+C’+D’)

3.26: Simplify the following Boolean function using the map presented in Fig : 3.30(a) and repeat using the map of figure 3:30(b)

F(A,B,C,D)=m1+m2+m3+m5+m7+m9+m10+m11+m13+m15

        F=D+BC'

    F=D+BC'









Tags:

Post a Comment

0 Comments